آنالیز مودال چیست ؟
اغلب اوقات مردم یک سری سؤالات سادهای در مورد آنالیز مودال و ارتعاش سازهها میپرسند که برخی وقتها جواب دادن به آن نیازمند پیشینه تئوری در این ارتباط است. هر چند مباحث تئوری تا حدودی زیاد بوده و یادگیری آن زمانبر است؛ درحالیکه برخی از مفاهیم بدون در نظر گرفتن بحثهای تئوری و محاسبات ریاضی قابل بیان نیز میتواند باشد. در این مبحث هدف شرح این مفهوم بهصورت ساده و بدون استفاده از روابط ریاضی است.
تعریفی ساده از آنالیز مودال
اولین سوال این هست که آنالیز مودال چیست؟
بطور خیلی ساده تر آنالیز مودال فرایندی است که در آن در باره خواص دینامیکی یک سازه که شامل فرکانس طبیعی، ضریب میرایی و شکل مدهای مختلف است، بحث میگردد.
شرح مفهوم آنالیز مودال
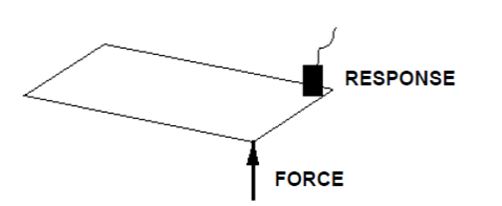
ورق تحت نیروی ضربه و اندازه گیری پاسخ ورق توسط سنسور شتاب سنج
فرض کنید یه صفحهای را داشته باشید (شکل 1) که یک نیروی ثابت به یک گوشه آن اعمال شود. ما معمولا در استاتیک حسی که از نیرو داریم این است که در اثر بارگذاری استاتیکی نیرو باعث تغییر شکل می گردد. درحالیکه در این مورد نیرو متغیر با زمان و بهصورت شبه سینوسی بر سازه اعمال میگردد. از آنجاییکه این نیرو متغیر بازمان است؛ در نتیجه در زمانهای خیلی پایین به عنوان نیروی ضربه عمل کرده و باعث تحریک ورق میگردد. در اثر این تحریک ورق شروع به ارتعاش خواهد کرد که با اندازه گیری پاسخ ورق در برابر نیروی تحریک میتوانیم مقادیر پاسخ را بر حسب شتاب توسط یک شتابسنج اندازهگیری و ثبت کنیم (شکل 2).
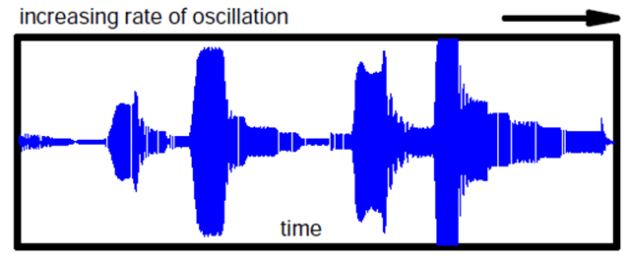
شتاب اندازه گیری شده در ورق
همانطوریکه در شکل دیده میشود با افزایش نرخ نوسان نیرو دامنه پاسخ ورق افزایش مییابد. این دامنه تا جایی ادامه پیدا میکند که کمکم نرخ نوسان نیرو به فرکانس طبیعی ورق نزدیکتر میشود که در این حالت ماکزیمم مقدار دامنه را از شتاب سنج ثبت خواهیم کرد. خیلی جالب است که مقدار نیرو ثابت نگهداشته شده است و صرفاً نرخ نوسان تغییر کرده است.
تابع پاسخ فرکانسی
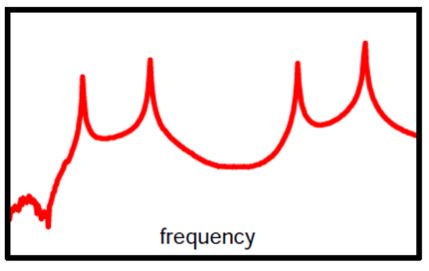
شکل 3-نمودار تابع پاسخ فرکانسی FRF
دادههای حوزه زمان اطلاعات مفیدی را با خود به همراه دارد؛ اما اگر این دادهها از حوزه زمان به حوزه فرکانس آورده شوند میتوانیم یک تابعی به اسم تابع پاسخ فرکانسی را نیز محاسبه کنیم (شکل 3). در این نمودار نتایج جالبی را میتوان به دست آورید. همانطوریکه در این نمودار دیده میشود در این تابع مقادیر ماکزیممی دیده میشود که بیانگر فرکانسهای طبیعی سیستم است. به این نکته هم باید توجه کرد که فرکانس نرخ بارگذاری یا تحریک بر روی پدیدار شدن ماکزیمم دامنهها در تابع FRF تأثیر بسزایی دارد. همانطوریکه در شکل 4 دیده میشود با افزایش فرکانس تحریک فرکانسهای طبیعی بیشتری مشاهده میشود بهعبارتدیگر اگر فرکانس تحریک کاهش پیدا کند در این صورت ممکن است برخی از فرکانسهای طبیعی در تابع FRF ظاهر نشوند.
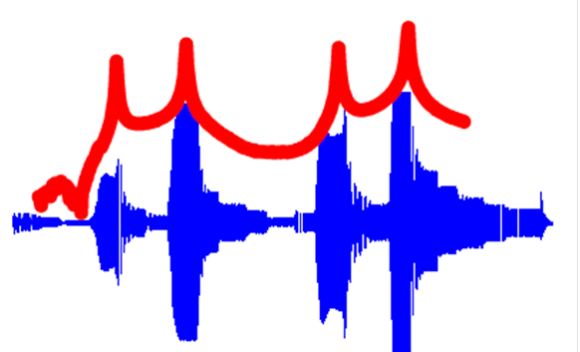
نمایش تابع پاسخ فرکانسی و زمان در کنار همدیگر.
نظر شما درباره این مطلب چیست؟
از ۱ تا ۵ ستاره به ما امتیاز بدید.
میانگین رتبه / 5. تعداد امتیازات کاربران:
امتیازی داده نشده، اولین نفری باشید که ثبت امتیاز میکنید